Тема 1.2: Плоска система сил.

План

1.  Система збіжних сил. Геометричний та аналітичний способи визначення рівнодійної системи збіжних сил.

2.  Геометрична та аналітичні умови рівноваги плоскої системи збіжних сил. Раціональний вибір координатних осей.

3. Додавання паралельних сил.

4. Момент сили відносно точки.

5. Пара сил. Момент пари сил. Властивості пар. Додавання пар. Умова рівноваги плоскої системи пар.

6. Теорема про паралельне перенесення сили. Зведення плоскої довільної системи сил до даного центра. Головний вектор та головний момент плоскої системи сил. Окремі випадки приведення плоскої системи сил до даного центра.

7. Умови рівноваги плоскої довільної системи сил, рівняння рівноваги. Рівновага плоскої системи паралельних сил. Раціональний вибір напряму координатних осей і центра моментів.

8. Визначення опорних реакцій балок.

9. В’язі з тертям.

1.  Система збіжних сил. Геометричний та аналітичний способи визначення рівнодійної системи збіжних сил.

Системою збіжних сил називаються сили, лінії дії яких перетинаються в одній  точці.

Система збіжних сил, лінії дії яких розміщені в одній площині, називається плоскою. Всі сили такої системи можна перенести вздовж ліній їх дій у спільну точку перетину цих ліній. Від цього дія даної системи сил на абсолютно тверде тіло не зміниться, що випливає з другої аксіоми статики. Отже, будь-яка система збіжних сил може бути замінена еквівалентною системою сил, які прикладені в одній точці.

Якщо на тіло діють дві сили та , які прикладені в одній точці О, то рівнодійна цих сил дорівнює їх геометричній сумі (рис. 1, а):

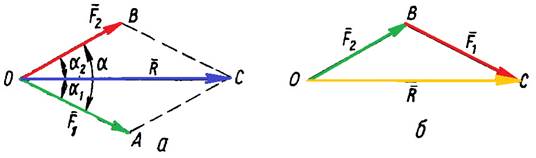
Рис. 1.

Для знаходження рівнодійної двох сил та , прикладених в одній точці О, не треба будувати весь паралелограм ОАСВ (рис. 1, а), а досить побудувати один з трикутників ОАС чи ОВС (рис. 1, б).

Трикутник ОВС (або ОАС) називають силовим трикутником, а такий спосіб додавання двох сил – правилом трикутника.

Якщо є кілька збіжних сил, то, застосовуючи послідовно правило додавання двох сил, роблять висновок, що рівнодійна кількох збіжних сил також дорівнює їх геометричній сумі (рис. 2):

тобто, щоб спростити запис, границі зміни індекс іноді опускають.

Рис. 2.

Рис. 3.

Многокутник ОАВСD (рис. 2), сторони якого у вибраному масштабі дорівнюють даним силам і однаково з ними направлені, називається силовим багатокутником.  У силовому багатокутнику стрілки завжди направлені одна за одною. Замикаюча сторона ОD силового многокутника направлена завжди від початку першої сили до кінця останньої і за модулем та за напрямом у вибраному масштабі вона зображає рівнодійну даної системи збіжних сил. Правило додавання  збіжних  сил  за  способом многокутника є загальним для складання будь-яких   векторів і називається геометричним додаванням.

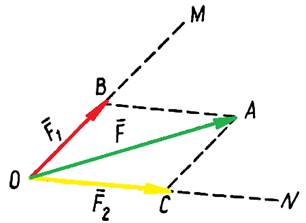
Розкладання сили на складові є оберненою дією додавання сил. Особливо часто доводиться розкладати задану силу на дві складові по двох заданих напрямах ОМ та ОN (рис.3). Для цього з кінця А вектора сили проводимо прямі АВ і АС, які відповідно паралельні прямим ОN і ОМ, і отримаємо паралелограм ОВАС. Сила , очевидно, буде діагоналлю цього паралелограма. Вектори і  є шуканими складовими силами.

Проекцією сили на вісь х називається відрізок між основами А₁ і В₁ перпендикулярів, опущених на цю вісь з початку і кінця сили (рис. 4, а). Точка А₁ буде початком, а В₁ – кінцем проекції. Проекція буде додатною, якщо її напрям збігається з додатним напрямом осі, якщо ж ні, то від'ємна.

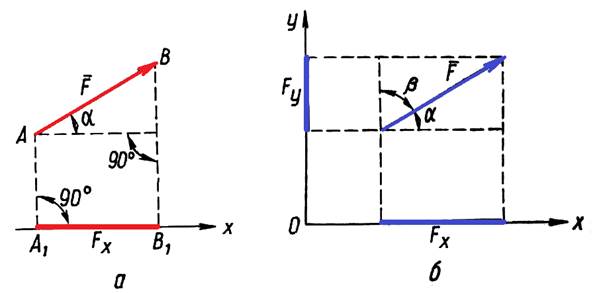
Рис. 4.

Із рис.4, б видно, що залежність між проекцією і величиною проектованої сили визначається рівністю

де α – кут між силою і додатним напрямом осі.

Очевидно, при α < 90° і α > 270° проекція сили на вісь буде додатною, а при 90° < α < 270° – від'ємною. Якщо α = 90° або α = 270°, то проекція сили на вісь дорівнює нулю, оскільки сила перпендикулярна до осі. Величину сили можна знайти за її проекцією на дві взаємно перпендикулярні осі (х та у), користуючись теоремою Піфагора (рис.1.12, б):

Лінію дії і напрям сили визначають за допомогою косинусів кутів між силою і додатними напрямами осей проекцій:

Теорема: проекція рівнодійної на будь-яку вісь дорівнює алгебраїчній сумі проекцій складових сил на цю саму вісь.

Доведемо цю теорему. Для цього з сил побудуємо силовий многокутник АВСDЕ (рис.5.), в якому рівнодійна зображена вектором  .

Опустимо перпендикуляри на вісь х із усіх вершин цього многокутника. Тоді, позначивши проекції сил  на вісь х відповідно через , будемо мати:

Відрізки bс і dе від'ємні, оскільки вони направлені в бік, протилежний напрямові осі проекцій. Очевидно, що

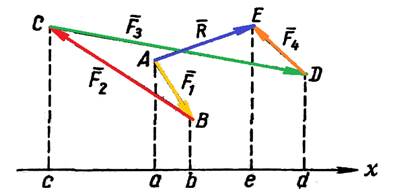
Рис. 5.

З рис.5 видно, що аb – bс = – ас;  – ас + сd = аd; аd – dе = аe. Але аe є проекцією рівнодійної на вісь x. Позначивши проекцію рівнодійної  на вісь x через , будемо мати: 

Отже, теорема доведена. Проекція рівнодійної на вісь х буде дорівнювати:

Спроектувавши цю саму систему сил на вісь у, перпендикулярну осі х, і застосувавши відповідні позначення, дістанемо:

Величину рівнодійної знаходимо за формулою:

Лінію дії і напрям рівнодійної знаходимо за допомогою косинусів кутів між рівнодійною і додатними напрямами осей:

2. Геометрична та аналітичні умови рівноваги плоскої системи збіжних сил. Раціональний вибір координатних осей.

Для рівноваги плоскої системи збіжних сил необхідно і достатньо, щоб рівнодійна сил дорівнювала нулю.

Згідно з двома способами визначення рівнодійної умова рівноваги плоскої системи збіжних сил може бути виражена у двох формах.

1. Умова рівноваги у геометричній формі.

Сили, лінії дії яких перетинаються в одній точці (рис. 6, а), будуть зрівноважені, очевидно, тоді, коли їх рівнодійна буде порівнювати нулю. У такому випадку довжина замикаючої сторони силового многокутника повинна дорівнювати нулю, тобто силовий многокутник буде замкнутим (рис. 6, б).

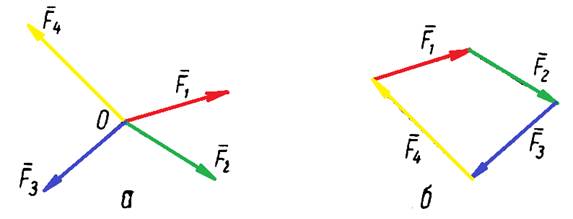
Рис. 6.

Отже, геометрична умова рівноваги збіжних сил, що лежать в одній площині, полягає в тому, щоб многокутник сил був замкнутим або інакше: збіжні сили, що розміщені в одній площині, перебувають у рівновазі, коли їх геометрична (векторна) сума дорівнює нулю:

2. Умова рівноваги в аналітичній формі.

Аналітично величина рівнодійної визначається за формулою:

Але коли , то нулю дорівнює і вираз під коренем, а це можливо тоді, коли кожна складова під коренем дорівнює нулю, тобто:

Ці рівняння називаються рівняннями рівноваги плоскої системи збіжних сил.

Отже, для рівноваги плоскої системи збіжних сил необхідно і достатньо, щоб алгебраїчні суми проекцій всіх сил на кожну з двох координатних осей, що лежать у площині дії сил, дорівнювали нулю.

Рівновага трьох непаралельних сил, що розміщені в одній площині.

Теорема: Якщо три непаралельні сили, що розміщені в одній площині, взаємно зрівноважуються, то лінії дії їх перетинаються в одній точці.

Нехай на тіло в точках А₁, А₂ та А₃ діють три непаралельні сили , і , що взаємно зрівноважуються і розміщені в одній площині (рис. 7). Лінії дії двох сил, наприклад  і , очевидно, перетинаються в одній точці А. Переносимо ці сили вздовж їх ліній дії в точку А та додаємо їх за правилом паралелограма. Тоді сила буде їх рівнодійною. Отже, на тіло тепер будуть діяти тільки дві сили:  та . Оскільки за умовою дані сили зрівноважуються, то вони повинні бути рівними за модулем і направлені по одній прямій у протилежні боки. Таким чином, лінія дії сили збігатиметься з лінією дії сили , а отже, проходитиме через точку А, в якій перетинаються лінії дії сил  і . Це й треба було довести.

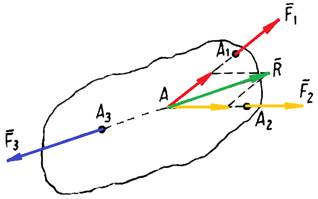
Рис. 7.

Ця   теорема   має  велике  методичне  значення при розв'язуванні задач статики. При цьому доцільно додержуватись такої методики.

1. З'ясовуємо рівновагу якого тіла треба розглянути, щоб розв'язати задачу, тобто знайти шукані величини. Звичайно розглядають рівновагу того тіла, до якого прикладені задані і шукані сили або сили, що дорівнюють шуканим (тобто, якщо треба знайти тиск на опору, то можна розглянути рівновагу тіла, до якого прикладена рівна цій силі реакція опори, і т. д.).

2.  Звільняємо тіло від в'язей і зображаємо на рисунку сили, що діють на тіло, і реакції відкинутих в'язей, зображуємо систему координат таким чином, щоб одна із невідомих реакцій була паралельна до однієї із осі (це спростить розв’язування рівнянь рівноваги).

3. До знайденої системи сил застосовуємо умови рівноваги, які відповідають цій системі.

4. Визначаємо шукані величини і досліджуємо результати.

При розв’язуванні задач на рівновагу плоскої системи збіжних сил необхідно раціонально розміщувати осі координат. Якщо одну із координатних осей розмістити вздовж лінії дії однієї із невідомих реакцій, то рівняння рівноваги можна буде розв’язати набагато простіше.

3.  Додавання паралельних сил.

При знаходженні рівнодійної двох паралельних сил, що діють на тверде тіло, сили можуть бути направлені: в одну і в різні сторони.

Додавання двох сил, що направлені в одну сторону (рис.8, а).

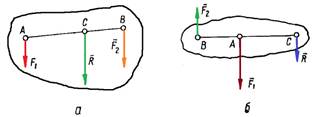
Рис. 8.

        Враховуючи властивості пропорції і рівності  ВС + АС = АВ  і  F₁ + F₂ = R , будемо мати:

Отже, рівнодійна двох паралельних сил, направлених в одну сторону, паралельна цим силам, направлена у ту саму сторону і дорівнює за модулем їх сумі; лінія дії рівнодійної цих сил проходить між точками прикладання складових сил на відстанях від цих точок, обернено пропорційних модулям сил.

Додавання двох сил, що направлені в різні сторони (рис. 8, б).

R = F₁ – F₂

Положення точки С вибирається так, щоб справджувалася рівність:

Отже, рівнодійна двох паралельних сил, які направлені в різні сторони,   паралельна  силам,   направлена в сторону більшої сили і дорівнює за модулем їх різниці; лінія дії рівнодійної проходить за більшою силою на  відстанях від складових,   обернено пропорційних цим силам.

За допомогою знайдених рівнянь можна розв'язувати задачі про розкладання даної сили на дві паралельні їй сили, що направлені в одну або в різні сторони.   

4. Момент сили відносно точки.

Поняття моменту сили можна застосувати до сил, що прикладені до всякого твердого тіла. Момент сили можна визначити відносно будь-якої точки, яку називають центром моменту.

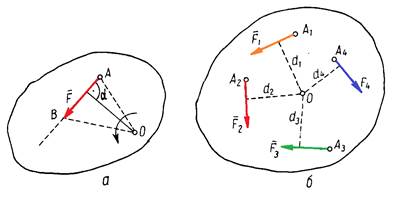
Рис. 9.

Моментом сили відносно будь-якої точки на площині називається добуток модуля сили на її плече відносно цієї точки, взятий із знаком плюс або мінус (рис. 9, а):

Момент сили вважається додатним, якщо сила намагається повернути тіло відносно точки О (центра моменту) проти обертання годинникової стрілки, а від'ємним – за стрілкою.

Чисельно момент сили Р відносно точки О дорівнює подвоєній площі трикутника АОВ:

де  А і В – початок і кінець сили;  О –  центр моменту.

Якщо лінія дії сили проходить через точку О, то d = 0 і момент сили відносно цієї точки дорівнює нулю.

Одиниця моменту дорівнює добуткові одиниці сили на одиницю довжини. Якщо силу вимірювати в кілограмах (кГ), а плече – в метрах (м), то момент сили буде в кілограмометрах (кГм); якщо силу вимірювати в ньютонах (Н), а плече – в метрах (м), то момент сили буде в ньютонометрах (нм):

1 кГм ≈ 9,81 нм.

Якщо до тіла прикладено кілька сил, що лежать в одній площині, то можна обчислити суму моментів цих сил відносно будь-якої точки О в цій самій площині (рис. 9, б). Отже,

Момент М₀, що дорівнює алгебраїчній сумі моментів даних сил відносно будь-якої точки О в тій самій площині, називають головним  моментом  сил відносно цієї точки:

Доведемо теорему Варіньона про момент рівнодійної:

Момент рівнодійної відносно будь-якого центра дорівнює алгебраїчній сумі моментів складових сил відносно того самого центра.

Нехай маємо сили , лінії дії яких перетинаються в точці А (рис. 10). Через будь-який центр О проведемо вісь Ох, перпендикулярну до прямої ОА. Щоб довести теорему, знайдемо відповідно вирази моментів

.

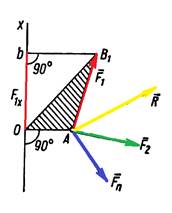
Рис. 10.

З рисунка видно, що

де  – проекція сили на вісь Ох.

Отже,

Так можна обчислити моменти всіх інших сил.

Позначимо рівнодійну сил  через , де .

Тоді за теоремою про проекцію суми сил на вісь дістанемо:

Помноживши обидві частини останньої рівності на ОА, матимемо:                                                                

Тоді

_, що є математичним виразом теореми Варіньона.

5. Пара сил. Момент пари сил. Властивості пар. Додавання пар.

Умова рівноваги плоскої системи пар.

Парою сил називається система, що складається з двох паралельних сил, рівних за модулем, але направлених в протилежні сторони (рис. 11).

 Рис. 11.

Пара сил намагається надати тілу обертального руху. Обертальна дія пари залежить від величини сили - F, плеча пари - h, напряму обертання, площини дії пари і характеризується моментом пари.

Плече пари – це найкоротша відстань між лініями дії сил пари. Момент пари дорівнює добутку модуля однієї зсил пари на плече пари:   M = F h.

Момент пари є додатним, якщо вона намагається обертати тіло в напрямі, протилежному руху годинникової стрілки.

Пару сил не можна зрівноважити однією силою, її можна зрівноважити тільки іншою парою. Алгебраїчна сума проекцій сил пари на вісь завжди дорівнює нулю.

Теорема про еквівалентні пари: дві пари, що лежать в одній площині, еквівалентні, якщо вони мають однакові алгебраїчні моменти.

Наслідки:

1. не змінюючи механічного стану тіла, пару сил можна  перемістити як завгодно в площині її дії;

2. не змінюючи механічного стану тіла, можна змінити модуль сил і плече пари, але так щоб її момент залишався  не змінним;

3. щоб задати пару, досить задати її момент.

Теорема про додавання пар: система пар, що лежать в одній площині, еквівалентна одній парі, що лежить в тій самій площині і має момент, який дорівнює алгебраїчній сумі моментів складових пар.

.

Для рівноваги плоскої система пар сил необхідно і достатньо, щоб алгебраїчна сума моментів даних пар дорівнювала нулю.

6. Теорема про паралельне перенесення сили. Зведення плоскої довільної системи сил до даного центра. Головний вектор та головний момент плоскої системи сил. Окремі випадки приведення плоскої системи сил до данного центра.

Доведемо теорему: механічний стан тіла не порушиться, якщо силу  перенести паралельно самій собі в будь-яку точку твердого тіла, додаючи при цьому пару сил, алгебраїчний момент якої дорівнює алгебраїчному моменту перенесеної сили відносно точки, в яку сила переноситься.

Нехай на тверде тіло діє сила F, прикладена в точці А (рис.12, а). Дія цієї сили не зміниться, якщо в будь-якій точці В тіла прикласти дві зрівноважені сили F' і F" так, щоб F' = F, а F" = - F. Одержана система трьох сил являє собою силу F', що дорівнює F, але прикладену в точці В, і пару (F,F"), момент якої  М = М_В(F).

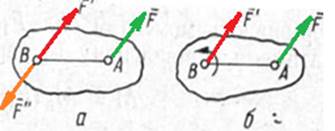
Рис. 12.

Отже, теорему доведено.

Пара сил (F, F") називається приєднаною парою сил.

Зведення плоскої системи сил до даного центра.

Нехай на тверде тіло діють сили F₁, F₂, F₃, що лежать в одній площині (рис. 13, а). Візьмемо в цій площині будь-яку точку О, яку назвемо центром зведення, і на підставі доведеної вище теореми перенесемо всі сили в центр О, добавивши при цьому систему трьох пар сил. Моменти  цих пар  дорівнюють  моментам сил F₁, F₂, F₃   відносно центра зведення О.

Додаючи сили F₁, F₂, F₃    за правилом  многокутника, дістанемо їх рівнодійну R^’ , що дорівнює геометричній сумі сил.

.

 Геометрична сума всіх сил системи називається головним вектором системи сил. Модуль і напрямок головного вектора не залежать від центру зведення.

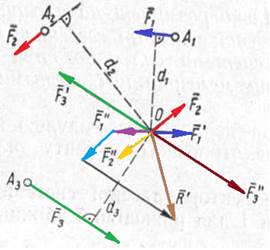
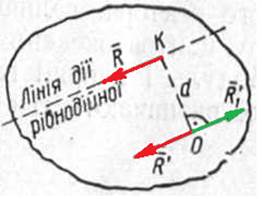
а б

Рис. 13.

Модуль і напрям головного вектора плоскої системи сил визначається так само, як і для рівнодійної системи збіжних сил

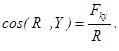
Плоска система пар еквівалентна одній парі, момент якої дорівнює алгебраїчній сумі моментів даних пар.

.

Цю пару з моментом М називають головним моментом заданої системи сил.

Таким чином, сили, що довільно розміщені на площині, можна звести до однієї сили, прикладеної в центрі зведення, яка дорівнює головному вектору даної системи сил, і до пари сил з моментом, що дорівнює головному моменту цієї системи сил відносно центра зведення.

Розглянемо можливі випадки зведення сил, що довільно розміщені на площині.

Випадок 1. Якщо R = 0;  М0, то задана система сил зводиться до пари сил, момент якої дорівнює головному моменту сил відносно центра зведення.

Випадок 2. Якщо R0;  М = 0, то задана система сил зводиться до рівнодійної цієї системи сил, що за величиною і напрямом дорівнює головному вектору; лінія дії рівнодіючої проходить через центр зведення О.

Випадок 3. Якщо R0; М0. Задана система сил зводиться до однієї сили – рівнодійної цієї системи сил, що дорівнює головному вектору сил і прикладена в точці (рис.14, б) на відстані  від центра зведення  точки О.

Випадок 4. Якщо R = 0;  М = 0, то  плоска система довільно розміщених сил перебуває у рівновазі.

7. Умови рівноваги плоскої довільної системи сил, рівняння рівноваги. Рівновага плоскої системи паралельних сил. Раціональний вибір напряму координатних осей і центра моментів.

Плоска система довільно розміщених сил перебуває у рівновазі, коли головний вектор і головний момент системи дорівнюють нулю.

Отже, для рівноваги плоскої системи довільно розміщених сил необхідно і достатньо, щоб сума проекцій всіх сил на кожну з двох довільно вибраних координатних осей дорівнювала нулю і щоб алгебраїчна сума моментів всіх сил відносно будь – якої точки в площині також дорівнювала нулю.

Під час розв’язування деяких задач буває доцільно замість одного або двох рівнянь проекцій складати рівняння моментів.

Якщо одне рівняння проекцій замінити, то умови рівноваги плоскої системи довільно розміщених сил матимуть вигляд:

Якщо замінити два  рівняння проекцій, то умови рівноваги плоскої системи довільно розміщених сил матимуть вигляд:

В окремому випадку, коли на  тіло діє плоска система паралельних сил, напрям координатних осей можна вибрати так, щоб вісь Х була перпендикулярна до паралельних сил , а вісь У – паралельна їм. Тоді проекція кожної сили на вісь Х буде дорівнювати нулю; отже незалежно від того чи зрівноважується ця система сил, чи ні, завжди матимемо

Тому  для рівноваги паралельних сил, що лежать в одній площині, достатньо двох рівнянь .

Для рівноваги плоскої системи паралельних сил необхідно і достатньо, щоб алгебраїчна сума всіх сил дорівнювала нулю і щоб алгебраїчна сума моментів усіх сил відносно будь-якої точки площини також дорівнювала нулю.

8. Визначення опорних реакцій балок.

Зосереджені сили та розподілені навантаження.

Зосереджене навантаження - це вид зовнішнього навантаження, яке прикладено до деякої точки тіла. Ми розглядали сили, які були представлені у вигляді вектора, прикладеного до точки. Проте у природі існує велика кількість взаємодій тіл, які здійснюються не в точці і які не можна уявити у вигляді вектора, прикладеного до точки.

Такими силовими факторами є сили тиску рідини або газу на поверхню твердих тіл, сили тяжіння, як масові сили, електромагнітні сили тощо. А тому у теоретичній механіці вводиться поняття про розподілені сили, які діляться на поверхневі та об'ємні.

Поверхневі сили діють на деяку поверхню тіла. Об'ємні сили діють на кожний елемент об'єму тіла, яке розглядається. Прикладом таких сил є сила тяжіння.

У теоретичній механіці розглядається дія на тіло тільки зосереджених сил, які прикладені до абсолютно твердих тіл. А тому розподілене навантаження необхідно замінити його рівнодійною, тобто зосередженою силою. Введемо декілька загальних положень.

Розподілене навантаження – навантаження, яке безперервно діє на деякій площі тіла; характеризується його інтенсивністю q, тобто величиною сили, яка припадає на одиницю об'єму тіла (у випадку об'ємних сил), на одиницю площі (у випадку поверхневих сил) та на одиницю довжини (якщо поверхню, на яку діє навантаження, можна вважати лінією, тобто шириною поверхні можна знехтувати). В останньому випадку розподілене навантаження має назву плоского, на силових схемах воно зображується у вигляді епюри, тобто графіка інтенсивності навантаження, яке прикладене до лінійного контуру тіла.

У загальному випадку розподілене навантаження зображується у вигляді певної кривої, що відображає даний закон зміни інтенсивності навантаження на ділянці тіла (рис. 14). Напрямок дії навантаження показується стрілками.

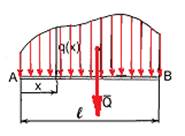
Рис. 14.

Спочатку будемо розглядати тільки рівномірно розподілене навантаження та навантаження, яке розподілене за лінійним законом. Замінюємо розподілене навантаження зосередженою силою.

Розглянемо ці два випадки:

1)  рівномірно розподілене навантаження (або навантаження, яке розподілене за законом прямокутника) показується на схемах у вигляді прямокутника, розміри якого такі: висота – це інтенсивність навантаження , довжина – це довжина l ділянки тіла, на якій діє навантаження. Стрілки показують напрямок дії навантаження (рис. 15). Для того, щоб замінити це навантаження рівнодійною силою , треба визначити її.  У даному випадку

де   q - інтенсивність навантаження, ;

       l - довжина ділянки тіла, на якій прикладене навантаження, [].

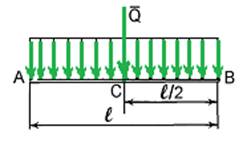
Рис. 15.

Точка С прикладання рівнодійної сили  розміщується посередині ділянки тіла, на якій діє навантаження. Тобто АС= l/2, а напрямок співпадає з напрямком розподіленого навантаження.

2) навантаження розподілене за лінійним  законом (тобто за законом трикутника). У цьому випадку (рис. 16) інтенсивність розподіленого навантаження на ділянці l змінюється від 0 до максимального значення .  Рівнодійна сила  від цього навантаження за величиною дорівнює:

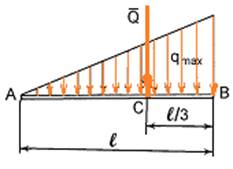
Рис. 16.

Точка С прикладання рівнодійної  розташована на відстані  або ,  а напрямок співпадає з напрямком навантаження.

Види опор балок.

З технічної точки зору опори конструкцій досить різноманітні. При формуванні розрахункової схеми все різноманіття існуючих опорних пристроїв схематизується у вигляді ряду основних типів опор, з яких найбільше часто зустрічаються: шарнірно-рухлива опора (можливі позначення для неї представлені на рис.17,а), шарнірно-нерухлива опора (рис.17,b) і жорстке защемлення або закладення (рис.17,с).

Рис. 17.

У шарнірно-рухливій опорі виникає одна опорна реакція, перпендикулярна опорної площини. Така опора позбавляє опорний переріз одного ступеня волі, тобто перешкоджає зсуву в напрямку опорної площини, але допускає переміщення в перпендикулярному напрямку й поворот опорного перерізу.

У шарнірно-нерухливій  опорі виникають вертикальна й горизонтальна реакції. Тут неможливі переміщення по напрямках опорних стержнів, але допускається поворот опорного перерізу.

У жорсткому защемленні виникають вертикальна й горизонтальна реакції й опорний (реактивний) момент. При цьому опорний переріз не може зміщатися й повертатися.

Методика визначення опорних реакцій балок.

Для розв’язування задач на рівновагу плоскої довільної системи сил необхідно скласти розрахунково-силову схему задачі. Прикласти до осі балки задані активні сили. Далі умовно звільнити балку від в'язей і замінити їх відповідними реакціями в'язей. Таким чином, балка буде знаходиться у рівновазі під дією плоскої системи довільних сил. Для розв'язання задачі потрібно використати умови рівноваги, скласти рівняння рівноваги і розв’язати їх.

9. В’язі з тертям.

Тертям називається опір, що виникає при переміщенні одного тіла по поверхні іншого. Залежно від характеру цього переміщення розрізняють два види тертя : тертя ковзання і тертя кочення.

Тертям ковзання називається опір, що виникає при ковзання одного тіла по поверхні іншого.

Основною причиною тертя є те, що поверхні стичних тіл не абсолютно гладкі, а в тій чи іншій мірі шорсткі. Тому при переміщенні одного тіла по поверхні іншого потрібна деяка сила для подолання опору, що чинять мікроскопічні нерівності поверхонь.

Мащення тертьових поверхонь значно зменшує тертя, оскільки масло заповнює всі нерівності і безпосереднє тертя поверхонь замінюється ковзанням їх по маслу і ковзання шарів між собою.

Сила тертя, що виникає при відносному спокої тіла, називається тертям спокою, а сила тертя, що діє під час ковзання тіла, називається тертям руху.

Якщо позначити через F максимальну величину сили тертя спокою, а через R_п  нормальну реакцію опорної поверхні, то на підставі цього закону матимемо:

F=f R_п ,

де:  f – коефіцієнт пропорційності, що називається коефіцієнтом тертя ковзання.

Опір, що виникає під час кочення одного тіла по іншому, називається тертям кочення. Цей опір обумовлюється деформаціями цих тіл. Тому точка прикладання нормальної реакції зміщується так, що виникає пара сил, яка називається парою тертя кочення.

Максимальна величина плеча цієї пари, що залежить від матеріалу заданих тіл, називається коефіцієнтом тертя кочення, який має розмірність довжини. Максимальна величина моменту пари тертя кочення дорівнює:

М_k=kN,

де  N – нормальна реакція;

k – коефіцієнт тертя кочення.

Запитання для самоконтролю:

1. Яку систему сил називають системою збіжних сил?

2. Для чого і яким чином будується силовий багатокутник?

3. Як формулюється умова рівноваги системи збіжних сил у геометричній формі?

4. Як формулюється теорема про рівновагу тіла під дією трьох непаралельних сил?

5. Як визначаються проекції сили на вісь і площину?

6. Який напрям має сила, якщо її проекція на вісь дорівнює нулю?

7. Як визначити силу за її проекціями?

8. Чому дорівнює проекція рівнодійної сили на вісь через її складові?

9. Як знайти аналітично рівнодійну силу?

10. Які умови і які рівняння рівноваги системи збіжних сил?

11. Чому дорівнює рівнодійна двох однаково спрямованих паралельних сил ?

12. Чому дорівнює рівнодійна двох протилежно спрямованих паралельних сил ? Де знаходиться точка її прикладення ?

13. Що таке момент сили відносно центра (точки)?

14. Куди спрямований вектор моменту сили відносно точки ?

15. Що таке пара сил, або просто пара ?

16. Які властивості має пара сил у площині ?

17. Як визначити момент пари?

18. Яка умова рівноваги системи пар у площині ?

19. Які дві пари є еквівалентними ?

20. Сформулюйте теорему про паралельне перенесення сили.

21. Що таке головний вектор і головний момент  плоскої системи довільних сил ?

22. В якому випадку плоска система сил зводиться до рівнодійної ?

23. В якому випадку плоска система довільних сил зводиться до однієї пари ?

24. Чи залежить головний вектор від вибору центра зведення ?

25. Сформулюйте теорему Варіньона про момент рівнодійної сили відносно центра.

26. Яка умова рівноваги для плоскої системи довільних сил ?

27. Скільки рівнянь рівноваги можна скласти для плоскої системи паралельних сил ?

28. Що таке зосереджене та розподілене навантаження ?

29. Як замінити рівномірно розподілене навантаження зосередженою силою ?

30. Які види опор ви знаєте ?

31. Що називається тертям ковзання ?

32. Що називається тертям кочення ?

Попередня тема Теоретичні відомості Наступна тема