Тема 1.3: Просторова система сил.

План

1. Паралелепіпед сил. Рівновага просторової системи збіжних сил.

2. Момент сили відносно осі.

3. Загальний випадок дії просторової системи сил на тіло. Рівновага довільної просторової системи сил. Рівновага просторової системи паралельних сил.

1. Паралелепіпед сил. Рівновага просторової системи збіжних сил.

Систему сил, лінії дії яких лежать у різних площинах, називають просторовою системою сил.

Просторові системи сил, як і плоскі, можна поділити на три види: просторову систему збіжних сил, систему сил, що довільно розміщені в просторі, і просторову систему паралельних сил.

Візьмемо силу , вектор якої довільно розташований у просторі (рис. 1). Виберемо у просторі прямокутну декартову систему координат , початок відліку якої (точку ) суміщений з точкою прикладання вектора сили . Спроектуємо вектор сили  на площину . Опустимо з точки  (кінець вектора сили) на вказану площину перпендикуляр, який перетинає її в точці . На площині  утворено вектор , який і є проекцією  сили на площину. За модулем ця проекція дорівнюватиме

,

де  - кут між вектором сили  та площиною.

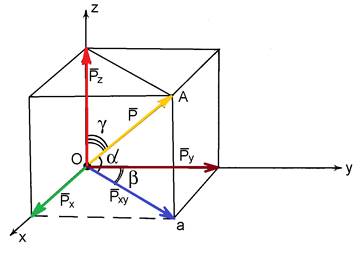
Рис. 1.

Якщо в площині  позначити кут , то є можливість спроектувати силу  на осі  та , опускаючи з точки  на осі перпендикуляри і за відомим вже правилом отримати проекції вектора  на вказані осі:

,

.

У даному випадку крізь вісь  та вектор сили  можна провести площину, тому є можливість спроектувати силу на цю вісь за відомим правилом. Ця проекція буде дорівнювати

,                                                 

де  - кут між вектором сили  та віссю  .

Рівнодіюча просторової системи сил, що сходяться в одній точці, прикладена в тій самій точці і рівна по модулю та напрямку діагоналі паралелепіпеда, ребра якого рівні та паралельні заданим силам.

Для рівноваги просторової системи збіжних сил необхідно і достатньо, щоб суми проекцій всіх сил на кожну з трьох координатних осей дорівнювали нулю.

;                    ;                   .

2. Момент сили відносно осі.

Для випадку довільної просторової системи сил необхідно знати поняття про момент сили відносно осі,  який характеризує обертальний ефект, що створюється силою, яка намагається повернути тіло навколо даної осі.

Щоб обчислити момент сили F відносно осі Z, треба спроектувати цю силу на площину І, перпендикулярну до осі, а потім обчислити момент цієї проекції F₁  відносно точки О — перетину осі Z з площиною І (рис. 2).

Отже, моментом сили відносно осі називається взятий із знаком плюс або мінус добуток модуля проекції сили на площину, перпендикулярну до осі, на її плече d1  відносно точки О перетину осі з площиною:

.

Момент сили відносно осі будемо вважати додатним,  якщо, дивлячись назустріч осі Z, можна бачити проекцію сили так, що вона намагається обертати площину І навколо осі Z проти руху годинникової стрілки. У протилежному випадку момент вважається від'ємним.

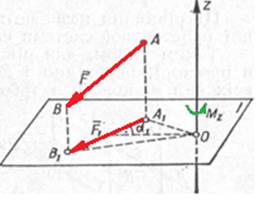
Рис.2

       Момент сили відносно осі зображається відрізком, відкладеним на осі Z від точки О в додатному напрямі, якщо Мz(F) > 0, і у від'ємному, якщо Мz(F)< 0.

Значення моменту сили відносно осі можна також виразити подвоєною площею трикутника А₁ОВ₁:    Мz (F) = ± 2 А₁ОВ₁.

Момент сили відносно осі дорівнює нулю у двох випадках:

а) якщо F₁ = 0, тобто лінія дії сили паралельна осі;

б) якщо d₁ = 0, тобто лінія дії сили перетинає вісь.

3. Загальний випадок дії просторової системи сил на тіло. Рівновага довільної просторової системи сил. Рівновага просторової системи паралельних сил.

Умови рівноваги довільної просторової системи сил.

Для рівноваги тіла, під дією системи сил довільно розміщених у просторі, необхідно, щоб воно не могло переміщатись вздовж кожної з трьох координатних осей.

Для цього треба, щоб:

;        ;      .

Крім того, треба, щоб тіло не мало змоги обертатись навколо кожної з цих трьох осей ; тому повинні справдитись такі умови:

;       ;         .

Таким чином, для рівноваги системи сил, довільно розміщених у просторі, необхідно і достатньо, щоб алгебраїчна сума проекцій всіх сил на кожну з трьох довільно вибраних координатних осей і алгебраїчна сума моментів всіх сил відносно кожної з цих осей дорівнювала нулю.

Коли всі сили, що діють на тіло, паралельні у просторі, то можна вибрати координатні осі так, щоб одна із осей (наприклад   Z) була паралельна силам. Тоді проекції кожної з сил на осі Х і У та їх моменти відносно осі Z будуть дорівнювати нулю і система рівнянь зведеться до трьох умов рівноваги

 ;       ;        .

Решта три рівняння будуть являти собою тотожності.

Отже, для рівноваги просторової системи паралельних сил необхідно і достатньо, щоб алгебраїчна сума проекцій всіх сил на вісь, паралельну силам, і алгебраїчна сума моментів всіх сил відносно кожної з двох осей, що лежать в площині, перпендикулярній до даних паралельних сил, також дорівнювали нулю.

Запитання для самоконтролю:

1. Назвіть умову рівноваги для просторової системи збіжних сил ?

2. Як розкласти силу, розміщену в просторі на три складові ?

3. Чому дорівнює рівнодіюча для просторової системи збіжних сил ?

4. Що називається моментом сили відносно осі ?

5. У яких випадках момент сили відносно осі дорівнює нулю ?

6. Назвіть умову рівноваги для просторової системи довільних сил ?

7. Назвіть умову рівноваги для просторової системи паралельних сил ?

Попередня тема Теоретичні відомості Наступна тема