Тема 1.8: Плоскопаралельний рух твердого тіла.
План
1. Плоскопаралельний рух твердого тіла.
2. Розкладання плоскопаралельного руху на поступальний та обертальний.
3. Швидкості точок плоскої фігури.
4. Поняття про миттєвий центр швидкостей.
1. Плоскопаралельний рух твердого тіла.
Плоско паралельним рухом твердого тіла називають такий рух, в якому всі точки тіла переміщуються в площинах, паралельних якійсь площині, яку називають основною. Прикладами плоско-паралельного руху можуть бути рух колеса на прямолінійній ділянці шляху, рух шатуна кривошипно-повзункового механізму.
З означення плоско паралельного руху випливає, що будь-яка пряма АВ, проведена в тілі перпендикулярно до основної площини, рухається поступально.
2. Розкладання плоскопаралельного руху на поступальний та обертальний.
Вивчення плоско паралельного руху зводиться до вивчення руху плоскої фігури S в її площині Q (рис.1). Цей рух можна розкласти на два: поступальний разом з полюсом, обертальний навколо полюса.
Рух відносно нерухомої системи координат називають абсолютним. Рух відносно рухомої системи координат називають відносним. Рух рухомої системи координат відносно нерухомої називають переносним. Абсолютний рух точки складний, він містить у собі відносний і переносний рухи.
Полюсом називається довільна точка, яка зв’язана з рухомою фігурою і яка приймається за центр повороту. За полюс можна вибрати будь-яку точку плоскої фігури.
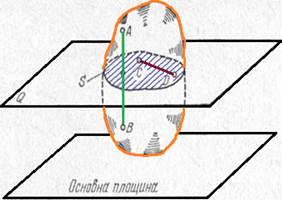
Рис.1
Кутова швидкість 
і кутове прискорення 
плоскої фігури також не залежать від
вибору полюса і є при плоско паралельному русі твердого тіла спільною
кінематичною характеристикою всіх точок тіла. Кутова швидкість у плоско
паралельному русі називається миттєвою кутовою
швидкістю, а кутове прискорення – миттєвим
кутовим прискоренням.
3. Швидкості точок плоскої фігури.
За полюс можна прийняти деяку точку А фігури (рис.2). Тоді швидкість будь-якої іншої точки В цієї фігури, згідно з теоремою про додавання швидкостей, буде складатися із швидкості VA точки А (при поступальному русі швидкості всіх точок тіла однакові) і швидкості обертального руху VBA точки В навколо точки А, тобто:
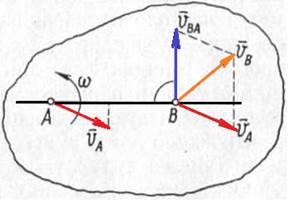
Рис.2
Вектор VBA направлений перпендикулярно до радіуса обертання АВ у бік обертання, а за модулем
де ω – кутова швидкість обертального руху плоскої фігури.
Теорема про швидкості точок плоскої фігури: швидкість будь-якої точки плоскої фігури дорівнює геометричній сумі швидкості полюса і обертальної швидкості цієї точки навколо полюса.
4. Поняття про миттєвий центр швидкостей.
Простим методом визначення швидкостей точок при плоскопаралельному русі тіла є метод миттєвих центрів швидкостей (м. ц. ш.).
М. ц. ш. називають зв’язану з плоскою фігурою точку, швидкість якої в даний момент часу дорівнює нулю.
1) швидкість миттєвого центра дорівнює нулю; 2) миттєвий центр лежить на перпендикулярі, опущеному з точки на напрям її швидкості; 3) швидкість точки дорівнює добутку миттєвої кутової швидкості на відстань точки від миттєвого центра швидкостей (рис.3)
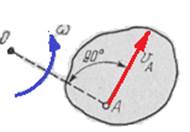
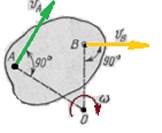
Рис.3 Рис.4
1. Відомі миттєва кутова швидкість ω і швидкість VА якоїсь точки А плоскої фігури (рис.3). У цьому випадку миттєвий центр швидкостей О міститься на перпендикулярі, опущеному з точки А на вектор швидкості VА на відстані
.
2. Відомі напрями швидкостей двох точок А і В плоскої фігури (рис.4).
Тоді миттєвий центр О лежить на перетині перпендикулярів, опущених з точок А і В на напрями їх швидкостей, причому
,
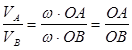тобто швидкості точок плоскої фігури прямо пропорційні їх відстаням від миттєвого центра швидкостей.
3. Відомо, що швидкості двох точок А і В плоскої фігури паралельні між собою, однаково напрямлені і перпендикулярні до відрізка АВ, але різні за модулем (рис.5). Тоді миттєвий центр швидкостей О лежить у точці перетину прямої, яка сполучає початки векторів VА і VВ з прямою, яка сполучає кінці цих векторів. Якщо вектори швидкостей точок А і В між собою рівні, то миттєвий центр швидкостей у даний момент лежить у нескінченності, миттєва кутова швидкість дорівнює нулю, швидкості усіх точок плоскої фігури будуть однакові і тому рух буде миттєво поступальним.
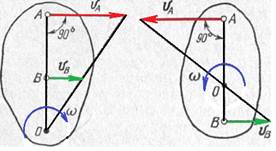
Рис.5 Рис.6
4. Відомо, що швидкості точок А і В плоскої фігури паралельні між собою, мають протилежні напрями і перпендикулярні до відрізка АВ (рис. 6). У цьому випадку миттєвий центр швидкостей О міститься у точці перетину відрізка АВ з прямою, яка сполучає кінці векторів VА і VВ.
5. Відомо, що плоска фігура котиться без проковзування по нерухомій кривій. Тоді миттєвий центр швидкостей О лежить у точці дотику фігури і кривої, оскільки швидкість цієї точки фігури в даний момент дорівнює нулю.
На закінчення розглянемо кочення колеса по прямолінійній рейці за різних умов тертя. На рис. 7 показано положення миттєвого центра швидкостей і графіки швидкостей точок вертикального діаметра для випадку тертя ковзання, тертя кочення, тертя кочення з проковзуванням, часткового і повного буксування колеса.
Ковзання Кочення Кочення з проковзуванням
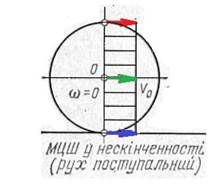
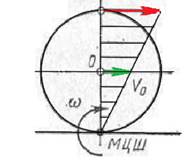
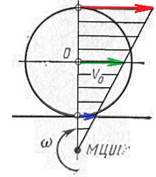
Часткове буксування Повне буксування
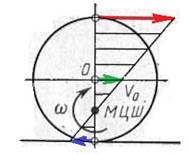
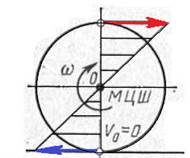
Рис.7.
Запитання для самоконтролю:
1. Який рух називається плоскопаралельним ?
2. Який рух називається абсолютним ?
3. Який рух називається відносним ?
4. Який рух називається переносним ?
5. Чи залежить обертальний рух навколо полюса від вибору полюса ?
6. Що називається полюсом при плоскопаралельному русі ?
7. Сформулюйте теорему про швидкості точок плоскої фігури.
8. Сформулюйте теорему про проекції швидкостей двох точок плоскої фігури на пряму, що з'єднує ці точки.
9. Яку точку називають миттєвим центром швидкостей ?
10. Назвіть основні способи визначення положення миттєвого центра швидкостей плоскої фігури.