К і н е м а т и к а

Тема 1.5: Кінематика точки.

План

1. Предмет кінематики. Спокій і рух, відносність цих понять. Система відліку. Основні поняття кінематики: траєкторія, відстань, шлях, швидкість, прискорення.

2. Способи задання руху точки. Натуральний спосіб руху точки; швидкість та прискорення точки. Прискорення повне, нормальне, дотичне.

3. Види руху точки залежно від прискорення.

1. Предмет кінематики. Спокій і рух, відносність цих понять. Система відліку. Основні поняття кінематики: траєкторія, відстань, шлях, швидкість, прискорення.

Кінематикою називається розділ теоретичної механіки, в якому вивчається рух матеріальних тіл у просторі з геометричної точки зору, без врахування сил, що діють на них.

Рух у механіці - це зміна з часом положення даного тіла в просторі відносно інших тіл.

Щоб визначити положення рухомого тіла (або точки) в просторі будь-яку систему координат жорстко зв'язують з тим тілом, відносно якого вивчають рух. Цю систему координат називають системою відліку. Система  відліку може бути рухомою і умовно нерухомою. Рух тіла відносно нерухомої системи відліку називають абсолютним; а відносно рухомої відносним.

Рух тіла відбувається  в просторі з часом. Простір в механіці розглядають як тривимірний евклідовий простір. Час – це скалярна безперервно змінна величина, і його вважають незалежною змінною величиною.

Крива, яку описує точка при русі її в просторі відносно вибраної системи відліку, називається її траєкторією.

2. Способи задання руху точки. Натуральний спосіб руху точки; швидкість та прискорення точки. Прискорення повне, нормальне, дотичне.

Рух точки задається двома способами: натуральним і координатним.

При натуральному способі задається, траєкторія і рівняння руху по цій траєкторії, а також початок і напрям руху.

Рівняння руху в загальному випадку: 

,

де: S – відстань точки від початкового положення, що є функцією часу;

       t – час руху точки від початкового моменту.

Знаючи траєкторію руху точки і рівняння руху по цій траєкторії, можна визначити положення точки вбудь-який момент часу; для цього в рівняння  треба підставити час.

Координатний спосіб полягає у тому, що положення точки у системі відліку визначається трьома координатами X,Y,Z.

Рівняння руху точки у координатному вигляді ;  ;     , за допомогою їх в кожний момент часу можна визначити положення точки в просторі.

Якщо точка за довільно вибрані, але рівні проміжки часу проходить однаковий шлях, то рух її називається рівномірним, а в протилежному випадку - нерівномірним.

При рівномірному русі швидкість точки є сталою величиною, а при нерівномірному – змінною. Найпростіше швидкість точки визначається тоді, коли вона рухається рівномірно і прямолінійно. У цьому разі модуль швидкості дорівнює відношенню шляху S, пройденого точкою, до проміжку часу t, протягом якого рухалась точка:

При прямолінійному русі точки вектор швидкості буде направлений по прямолінійній траєкторії з даного положення точки вбік її руху.

При рівномірному прямолінійному русі, шлях S, пройдений точкою дорівнює добутку швидкості V точки на час її руху,  S = V·t,   це   рівняння  називають рівнянням рівномірно-прямолінійного руху точки.

Якщо в початковий момент часу (t = 0) точка М знаходиться від точки О на відстані S₀ = ОМ₀, тобто в точці М₀ (рис. 1), то рівняння руху матиме вигляд:  S = S₀ + V·t.

Тоді швидкість точки  дорівнює   

( м/с ),

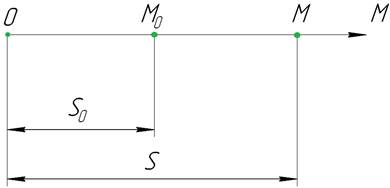
Рис.1

При нерівномірному русі розрізняють два поняття: середня швидкість і швидкість у даний момент.

Розглянемо, як визначається швидкість точки у загальному випадку нерівномірного криволінійного руху при натуральному способі визначення руху.

Позначимо проміжок часу, протягом якого відбувається рух, через . Знак  (грецька літера «дельта») означає приріст відповідної змінної величини (в даному випадку t). Нехай будь-яка точка М рухається по криволінійній траєкторії (рис. 2). У момент часу t ця точка займає на траєкторії положення М, а за проміжок часу пройде відстань і перейде в положення М₁. З'єднаємо точки М і М₁ вектором. Вектор ММ₁ називається вектором переміщення точки за деякий проміжок часу.

Середня швидкість точки буде визначатись так:

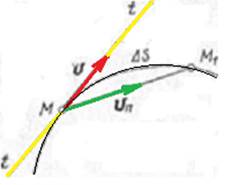
Рис.2

Переміщення точки ММ₁  є вектор, а тому вектор середньої швидкості точки має напрям вектора її переміщення, оскільки є скалярна величина.

     Якщо зменшувати проміжок часу, залишаючи незмінним початок цього проміжку, то безперервно буде зменшуватись і величина переміщення  ММ₁ =точки, а середня швидкість буде приближатись до значення швидкості точки в даний момент часу.

Швидкості точки в даний момент часу – це границя, до якої прямує середня швидкість, коли прямує до нуля.

Отже, швидкість V точки в даний момент часу дорівнює першій похідній за часом від дугової координати. Швидкість направлена по дотичній до траєкторії в бік руху точки.

Рівнозмінний рух – рух, за якого швидкість точки за однакові проміжки часу змінюється на однакову величину.

Величина, яка характеризує зміну вектора швидкості за модулем і напрямом, називається прискоренням.

У прямолінійному русі точки вектор швидкості завжди збігається з траєкторією і тому вектор зміни швидкості також збігається з траєкторією. Якщо за невеликий проміжок часу швидкість точки змінилася на , то середнє прискорення . Середнє прискорення не дає уявлення про дійсне прискорення у кожний даний момент часу (дійсне прискорення називають миттєвим). Дійсне прискорення – це границя, до якої прямує середнє прискорення при , що прямує до нуля:

,

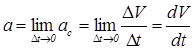Враховуючи, що ,   

дістаємо    

  (м/с²).

Дійсне прискорення в прямолінійному русі дорівнює першій похідній швидкості за часом або другій похідній координати (відстані від початку відліку переміщення) за часом.

Коли точка рухається по криволінійній траєкторії, то швидкість змінює свій напрям. Уявимо точку М, яка за час , рухаючись по криволінійній траєкторії, перемістилась у положення М₁ (рис. 3). Вектор приросту (зміни) швидкості позначимо , тоді   .

Щоб знайти вектор , перенесемо вектор V₁ у точку М і побудуємо трикутник швидкостей. Знайдемо вектор середнього прискорення: .

Вектор а_с паралельний вектору , оскільки від ділення векторної величини на скалярну напрям вектора не зміниться.                                                          

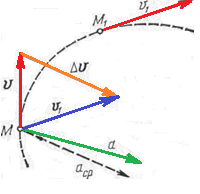
Рис. 3.

         Вектор дійсного прискорення — це границя, до якої прямує відношення вектора приросту швидкості відповідного проміжку часу, коли він прямує до нуля,    

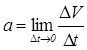
     Таку границю називають векторною похідною. Таким чином, дійсне прискорення точки в криволінійному русі дорівнює векторній похідній швидкості за часом.

З рис. 3 видно, що вектор прискорення в криволінійному русі завжди напрямлений у бік угнутості траєкторії.

Прискорення в криволінійному русі, якщо  рух точки задано звичайним способом, визначається за теоремою про проекції прискорення на дотичну і нормаль.

Проекцію повного прискорення на нормаль до траєкторії називають нормальним прискоренням; проекцію повного прискорення на дотичну до траєкторії називають дотичним прискоренням; його іноді називають ще тангенціальним.

Теорема. Нормальне прискорення  дорівнює квадрату швидкості, поділеному на радіус кривизни траєкторії у даній точці, дотичне прискорення дорівнює першій похідній швидкості за часом.

,             ,

Аналізуючи формули дотичного і нормального прискорень, можна побачити, що коли швидкість за модулем не змінюється, то = 0;  а коли швидкість не змінюється за напрямом (прямолінійний рух), то = 0.

Виходить, що дотичне прискорення характеризує зміну швидкості лише за модулем, а нормальне – лише за напрямом.

Знаючи дотичне і нормальне прискорення, можна визначити модуль і напрям повного прискорення за формулами: модуль прискорення    ;  

напрям прискорення 

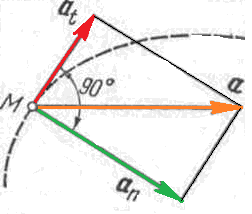
Рис. 4

Часто дотичне і нормальне прискорення розглядають не як проекції, а як складові повного прискорення, тобто як векторні величини. Коли осі взаємно перпендикулярні, то проекції вектора на ці осі і його складові, напрямлені по цих осях, рівні між собою за модулем. Дотичне, нормальне і повне прискорення показано на рис. 4.

Якщо  > 0, то вектори дотичного прискорення і швидкості напрямлені в один бік і тому рух буде прискореним. А коли  < 0, то вектор дотичного прискорення має протилежний до швидкості напрям і тому рух буде сповільненим. Вектор нормального прискорення завжди напрямлений до центра кривизни, тому це прискорення називають ще доцентровим.

3. Види руху точки залежно від прискорення.

Аналізуючи формули дотичного і нормального прискорень, можна зробити такі висновки:

1.  , , рух нерівномірний (Vсоnst), криволінійний ();

2. ,  , рух рівномірний (V = соnst), криволінійний ();

3. , , рух нерівномірний (Vсоnst), прямолінійний ();

4. , , рух рівномірний прямолінійний.

Під час рівномірного руху дотичне прискорення . Модуль швидкості точки в рівномірному русі – величина стала  = соnst.  Звідси  , інтегруючи цей вираз, дістаємо   

,      ,

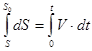Остаточно формули рівномірного руху :

V = соnst,  .

В рівно змінному русі дотичне прискорення – величина стала:

= соnst,  

звідси 

.

Інтегруючи цей вираз, дістаємо

,       .

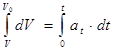Остаточно формула швидкості

.

Оскільки , інтегруючи цей вираз, дістаємо рівняння рівно змінного руху точки   

,         .

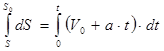Формули  рівно змінного руху:

;    

Якщо точка рухається криволінійно, то вона має нормальне прискорення    , а модуль повного прискорення визначається за формулою

.

Запитання для самоконтролю:

1. Що вивчає кінематика ?

2. Які існують системи відліку ?

3. Який рух називається рівномірним ?

4. Який рух називається рівнозмінним ?

5. Які є способи задання руху точки ?

6. Що називається швидкістю точки ?

7. Що називається прискоренням точки ?

8. Яке прискорення називається дотичним, а яке нормальним ?

9. Які існують види руху точки залежно від прискорення ?

Попередня тема Теоретичні відомості Наступна тема